統計学を学ぶがるたろう
今日は外でランチにきています
モニュモニュモニュ
うーん!ここのバナナクリームパスタ、最高に美味しいです!濃厚な味つけとフルーティな香りがたまらない!
ここはどれもハズレがないですね。ポメラステッド研究所の職員でも評判の店です。
口コミサイト見てみようっと
シバ先生見て見て!やっぱり星5つが多くてすごい評価が高いです!

口コミサイトでよく見る「棒グラフ」ですね。評価カテゴリ別の口コミ件数が表されていますね。
実はこれは、データの分布の可視化の1つです。分布の特徴をとらえるときの問いかけ「どんな値をとるか?」「各値の出やすさは?」に答えるグラフになっていますね。
これがデータの分布の可視化なんですね。
意外と身近にあったんですね!
この口コミのグラフを眺めるだけで、どんなお店なのか直感的に分かりますね。データの可視化の目的は、データとその元になる現実に対して直感的な理解を得ることです。
データの可視化とは棒グラフを使うことでしょうか?
質的データや離散的な値(とびとびの値)をとるデータの分布を可視化するには、棒グラフが使われます。
棒グラフの考え方を、連続的な値をとるデータにも使えるように拡張したものがヒストグラムです。
棒グラフとヒストグラム
ヒストグラムでやりたいことは棒グラフと基本的に同じですが、観測値をグルーピングするステップが1つ入ります。
どういうことか例で見ていきましょう。まず、先ほどの口コミサイトのように、以下のデータの棒グラフを作って見ましょうか。
5つ星口コミ評価のデータ (小さい順に並び替え済み)
1 1 2 2 2 2 3 3 3 3 3 3 4 4 4 5
横軸にカテゴリ(星の数)を書いて、
縦軸はそのカテゴリ別の観測値の数を数えてみましょう。
スター別の評価の件数が棒の高さになるわけですね!
カキカキカキ
よし、出来ました!こんな感じでしょうか!

うまく出来ましたね!
わーい!
では、次のようなデータだとどうでしょうか
バナナの長さ(cm)データ(小さい順に並び替え済み)
16.2 16.6 17.2 17.4 17.6 17.8 18.1 18.2 18.4 18.5 18.6 18.7 19.2 19.4 19.6 20.2
うわあ、やっぱり数字の羅列は目に厳しいな
よし!さっきと同じ要領で、、、
あれっ?5つ星のスターと違って全部違う値、、、各値が出た個数を棒グラフにすると、、、?
全部1個?何だかよくわからなくなりました、、、!

観測値が連続的な値をとるデータでは、少数をどこまでも細かく考えれば、観測値が厳密には全て異なります。(実際には観測の限界で丸まった数値になり同じに見えることがありますが)
そうすると口コミ評価のように、データの分布をとらえる棒グラフが作れないってことでしょうか。
そこで観測値をグルーピングする処理を入れるのです。
例えば、1cm刻みでグルーピングしましょう。16cm台、17cm台、18cm台、19cm台、20cm台の5つのグループに分かれます。
グルーピングするとは、17.2cmも17.8cmも同じ17cm台、とみなすといったように、同じグループに入った数値は同じ数値として扱うのです。
近い数値はざっくり同じとみなすんですね!
観測値が本来持っていた情報は一部失われることになりますが、その代わり棒グラフと同じようにデータの分布が描けるんです。
連続する数値に区切りを入れて、観測値をグルーピングしたあと、観測値の個数をカウントしたグラフをヒストグラムと言います。
グルーピングをしてから、もう一回グラフをチャレンジしてみます!
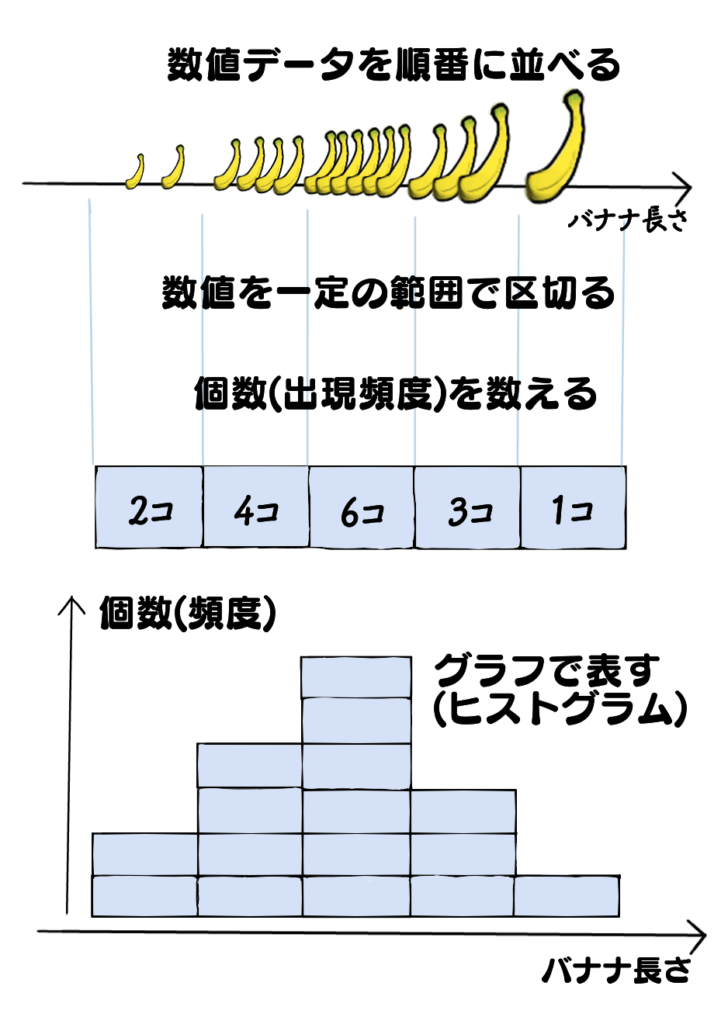
棒グラフと同じようなグラフになりました!
データの分布のカタチがイメージつきやすいです!
OKです!コツはつかめましたね!
- グルーピングした数値の範囲を「階級」や「クラス」と言います。
- 階級毎の観測値の個数を「度数」と言います。
注意点
ヒストグラムを作成する時は、注意点があることを知っておきましょう。数値のグルーピングの仕方です。
先ほど1cm刻みでグルーピングしましたが、0.1cm刻みや2cm刻みとすることもできます。
・・・そうするとグループ別の観測値の個数が変わるので、グラフのカタチが変わってしまいませんか?
その通りです。ヒストグラムは、グルーピングのとりかたによって、グラフの形が変わるといった注意点があります。

うにゅうにょカタチが変わるのは困りますね。グルーピングはどのように設定すべきなんでしょうか?
正解はなく、分析者が自由に決めるしかないのです。データの分布について何らかヒントが得られればヒストグラムの役割は果たしたことになり、厳密さの追求は必要ありません。
色々試してみるしかないんですね!データが増えてくると1つ1つグルーピングを考えるのが大変そうですね、、、
そうです。そこで、データの観測値に基づいてオススメのグルーピングの仕方を自動で提案してくれるアルゴリズムがいくつかあり、統計ソフトでは簡単に使えます。
そうなんですか!お任せコースは便利そうです!
詳しくは、統計ソフトRを使ったデータの可視化の練習(別の授業)の中で見ていきましょう。
本日は、ヒストグラムの考え方と注意点だけおさえてもらったら大丈夫です。
はい!
- オススメのグルーピングの仕方は「統計学(R実践編)」でご紹介します。以下の3つのやり方が統計ソフトRでは簡単に使うことができます。
- スタージェス(Sturges)の公式
- スコット(Scott)の選択
- フリードマン=ダイアコニス(Freedman-Diaconis)の選択
まとめ
本日はここまでにしておきましょう。データの分布の可視化として、ヒストグラムをご紹介しました。分析の出発点としてとてもよく使うグラフです。
棒グラフとの違いでヒストグラムのイメージを理解することができました!しっかり復習しておきます!
がるたろうは
今日もたくさん学べたようです!
- カテゴリ別の観測値の個数についての棒グラフを、連続的な値をとるデータにも使えるように拡張したものがヒストグラム
- ヒストグラムでやりたいことは棒グラフと基本的に同じだけど、観測値をグルーピングするステップが1つ入る。
- ヒストグラムは、グルーピングのとりかたによって、グラフの形が変わるといった注意点がある。オススメのグルーピングを提案してくれる「あるごりずむ」があるみたい。


