統計学を学ぶがるたろう
今日はモグラくんたちと遊んでいます
よーし、つかまえたぞ!

ハアハア
・・・ラスモグくん、つかまえました!
お疲れさまでした。「モグラくん捕獲ゲーム」、1セット目はなかなかハードでしたね。
楽しかったです!めっちゃのどかわいたー!

みんな捕獲ー!がしっ
2セット目はカンタンすぎました!
実は今回、モグラくんたちに協力してもらって、出現場所の違いで、異なるデータを表現してもらったんです。
私のいた場所が平均、出現場所が観測値とみなして、
1セット目が平均からのばらつきが大きいデータ
2セット目がばらつきが小さいデータ
を意味していたんです。

ばらつきの意味
バラツキが違うとゲームの面白さや難易度が全然変わってきますね!
そのとおりです。ばらつきが大きいデータは、その元となる現実にはドキドキ・ハラハラな側面があると言えるでしょう
ドキドキ・ハラハラ!
ばらつきが大きいことは、いい面と悪い面があります
まずはいい面から。ばらつきが大きい現実は、先がカンタンに読めないので、そのぶん面白いんです。
オフロードバイクやジェットコースターのコースはアップダウンが激しい方が面白いですよね。
映画とか漫画も、先が読めないドキドキハラハラな展開が良いですね!
他にもスポーツなどの勝負ごとでは、ムラっ気はあるけど、たまにとんでもない結果をだすプレイヤーがいれば、一か八かの大勝負を仕掛けられます。

- 金融の世界では、ばらつきの違いをそのままビジネスにしています。
- ばらつきが大きいことを、「リスク」が大きいと言います。
- 収益の変動が大きいけど儲ける時はすごく儲ける金融商品(ハイリスク・ハイリターン/新興国為替など)、収益の変動が小さいけど儲けは小さい金融商品(ローリスク・ローリターン/先進国の債券など)、といった、多様なバラエティを投資家に提供しています。
悪い面はその裏返しでしょうか?
そうです。ドキドキ・ハラハラなんていらない、安定・安心を求める現実の場面ではばらつきは小さい方がいいんです。
ビジネスにおいては、計画を立てて安定した経営を行うために、データのばらつきは小さくしたいことが多いです。
例えば自動車メーカーからすると、大きさがバラバラなタイヤを作ってくる工場は困りますよね。
サイズが合わないタイヤだと車が作れないです…!

ビジネスの生産現場では、データのばらつき状況をしっかり管理して、コントロールすることが大事なんです。
バラツキを今より小さくするためには、データの元にある現実に何らかの手を打つ必要があります。例えば新規設備の導入、マニュアルの整備、作業員の研修などなど。
データを通じて現実の改善点を考えていくんですね!
分散
それでは、データのばらつき具合を表す統計量を見ていきましょう。「分散」・「標準偏差」と呼ばれる統計量です。

ばらつきの統計量の計算には、個々の観測値が平均とどれくらい違う値をとっているかという情報を使います。前回平均を学んだ際に、このことを何といったか覚えていますか?
はい!偏差と言いました。観測値は平均+偏差と見れることも学びました。
「平均と偏差」の回より再掲載

その通りです。偏差の合計がどうなるかも覚えていますでしょうか?
はい!0になるんでした!平均は偏差の合計が0になるように決められた値だったからです。
「平均と偏差」の回より再掲載
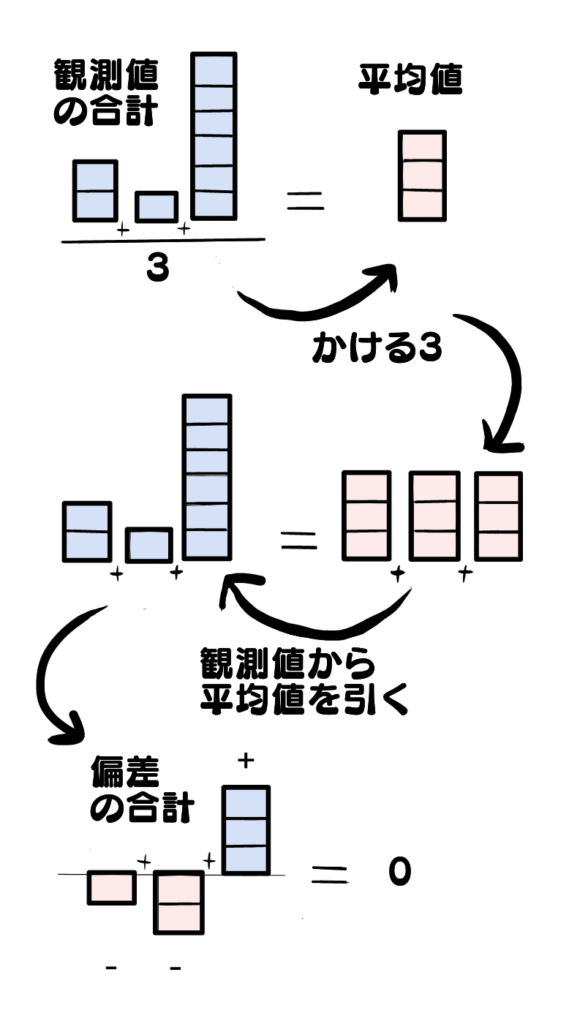
しっかり復習できてますね!
偏差はそのままだとプラスとマイナスで打ち消しあって使いにくいので、プラスの値に変換したいと思います。どのようなやり方が考えられるでしょうか?

「絶対値」をとるのはどうでしょうか?離れ具合を表す数字になると思います。
大変良いアイデアですね!シンプルに符号を全部プラスにすることで「平均からの距離」をそのまま表せますね。
他にもプラスの値にする方法は何かありそうでしょうか?
うーん、、、そうですね。。。
ちょっと思いつかないです
普通はあまり思いつきませんが、
「2乗」するというやり方なんです。
2乗は同じ数値を2回かけ算することですよね。確かにマイナスの数値もプラスになりますね。

絶対値の方が自然な気がしますね
せっかくの良いアイデアでしたが、
これから使うのは、2乗する方なんです。
そうなんですか!しょんぼり
数学的な扱いやすさが、1つの理由になります。
絶対値は、マイナスだったらプラスに、プラスの場合はそのまま、というように「符号による場合わけ」が必要ですが、これは数学的に扱いが難しいのです。
2乗では、元の数値がマイナスでもプラスでも、符号による場合分けは必要なく、ただ2回かけ算すればよいですね。
考える手間が省けるのですね!
- 他の理由もあります。グラフにすると絶対値は0でカクッと折れ曲りますが、2乗は0の近くでも滑らかになっています。これは、絶対値は0の境目において、「微分が不可能」という性質を表しています。
- 数学で重要な演算である「微分」が使えないことは、理論を展開する上で非常にやっかいなので、絶対値はよく敬遠されます。
- 参考ですが、もし、分布の代表値として平均ではなく、中央値を採用する場合、絶対値を使ったばらつきの統計量を考えることがあります(中央絶対偏差)。
観測値の偏差を2乗したあとはどうすればよいでしょうか?
ばらつきの統計量のゴールは、データの観測値の平均的なばらつき具合を、1つの数値で表現したいことです。1つの数値にするために何か思いつきますか?
偏差の2乗が観測値の数だけある状態なので、その平均をとる、ということでしょうか!
その通りです。これは分散と呼ばれます
平均からの離れ具合である偏差の2乗、これの平均をとった代表的な値が分散ということですね!
ここで注意が必要です。分析の目的によって平均をとる際の分母が変わるのです。(分子は偏差の2乗の合計で同じ)
!?観測値の数でわるんではないんですか?
結論からいうと、手元にあるデータだけで分析が完結する場合は、観測値の数「n」でわる、手元のデータを超えた範囲において判断や予測をする場合は、「n-1」でわるのです。

がるたろうくんの通う学校の先生が、必要な体操服のサイズを知るために、生徒の体長の分散を知りたい状況を例にとりましょう。
今在籍している生徒のみを考える場合、手元にある全生徒の体長データだけで分析が完結します。このような時は、観測値の個数nでわって問題ありません。
しかし、将来入学してくる生徒に関して予測や判断をしたい場合、つまりデータを超えた範囲で分析したい場合は、観測値の個数nから1を引いた数、n-1でわる方がよいのです。
目的によって変わるんですね!なんだか不思議ですが
なぜ、1をひくのかは、「データを使う」パートで詳しくご説明します。今は、目的によって分母が変わるということだけ頭にとどめておいてください。
はい!
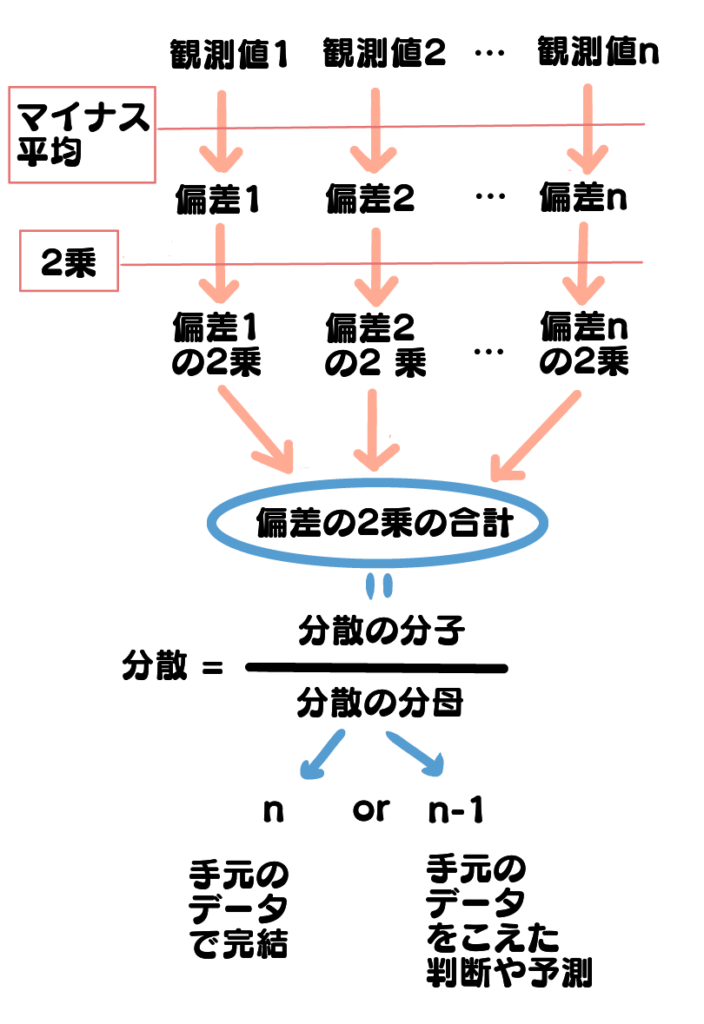
- n-1でわる分散は「普遍分散」とも呼ばれます。
- なぜ目的によって分散が変わるのか、手元のデータをこえた判断や予測を行う場合はなぜn-1でわるのか、その理由は「データを使う」パートにて詳しく説明していきます。
標準偏差
分散は2乗しているので、数値の意味としては分かりづらいですね、、、
数学的に扱いがラクになった分、現実の解釈が難しくなるという問題がないでしょうか?
いいところに気がつきましたね。分散は観測値の単位が2乗されていて、平均と単位が異なるので、平均からの離れ具合という直感的な理解ができません。
そこで、分散の単位を平均に合わせた「標準偏差」という数値を考えます。2乗する前の数値の世界に戻すのです。

数学では、足し算の逆は引き算、かけ算の逆はわり算、と言ったように、逆の演算手法が用意されています。2乗の逆となる演算は何がありましたでしょうか?
そうですね、、、
うー、、、学校で何か習ったような気がしますが、忘れちゃいました。。。
大丈夫ですよ。
平方根(ルート)という演算になります。
あっ「るーと」か!
意味としては、2乗したらその数字になるような元の数字を探すことでした。
その通りです。分散の平方根が「標準偏差」です。
平方根をとることで単位が平均とそろいますので、平均からの標準的な離れ具合という意味に解釈ができます
平方根はプラスとマイナスがあると思いますが、どちらを使えばよいでしょうか?
プラスの値を標準偏差とします。平均からの距離というイメージを持ってもらえればよいでしょう。距離は常にプラスですね。
わかりました!


標準偏差は、観測値が平均からざっくりどれくらい離れるものなのかの解釈を与えてくれます。
離れ具合の目安ができるわけですね。
平均と標準偏差を見るだけで、元の観測値全てを見なくても、データの違いが想像できます。
どんなデータなのか想像してみましょう
データA:平均10、標準偏差1.63
データB:平均10、標準偏差7
標準偏差が小さいデータは観測値がだいたい平均近くにあって、標準偏差が大きいと観測値は平均から広くばらけているイメージですね。
その通りです!イメージがしっかりできていますね

ちなみに元のデータはこんな感じでした
データA(平均10、標準偏差1.63):8, 9, 9, 10, 11, 13
データB(平均10、標準偏差7):0, 3, 8, 14, 15, 20
(ここは例として、観測値の数nで割った分散で計算している)
最後に、分散と標準偏差の使い分けについて触れておきましょう。
現実の解釈やコミュニケーションでは標準偏差が便利ですが、数学的な理論の展開や計算をしていくには分散の方が扱いやすいことがあります。
これから、文脈に応じて分散か標準偏差で表現を使い分けますが、データのばらつき具合を表す数値としては全く同じ情報で、意味は一緒です。混乱しないようにしましょう。
データのばらつきを言いたいときに、どちらで表現するかの違いだけということですね!
まとめ
本日はここまでにしておきましょう。データの分布のばらつきを表す統計量の分散・標準偏差をご紹介しました。
データの観測値のばらつき具合の表し方が学べました!分散・標準偏差といった新しい考え方をしっかり復習しておきます!
がるたろうは
今日もたくさん学べたようです!
- ばらつきが大きいデータは、その元となる現実には先が読めないドキドキ・ハラハラな側面がある。ビジネスの生産現場では、データのばらつき状況をしっかり管理して、コントロールすることが大事。
- ばらつきを表す統計量は、観測値の偏差を使う。偏差はそのままだとプラスとマイナスで打ち消しあってしまうので、二乗することでプラスにする。
- 偏差の二乗の平均を分散という。平均の分母は観測値の数nでわると思ったら、分析の目的によって変わるらしい。手元のデータで完結する時はnでわって、データの範囲を越える分析をする時はn-1でわると。
- 分散の平方根は標準偏差という。単位が平均とそろって、観測値が平均からざっくりどれくらい離れるものなのかという解釈がしやすい。


