統計学を学ぶがるたろう
ポメラステッド研究所の裏庭で
地面をならしています
ウンショ。ウンショ。ふう、こんなものかな?
どうもお疲れさまでした。デコボコだった地面がキレイなたいらになりましたね。
この「トンボかけ」作業は統計学を学ぶうえで何か意味があるんでしょうか?
本日のテーマである「平均」のイメージにぴったりなので、身体で覚えてもらいたかったのです。
えっトンボかけと平均が関係あるんですか!
平均
分布の特徴をとらえる方法として前回まで可視化を学びましたが、本日から統計量のアプローチを学びます。
分布の特徴を凝縮した値を作る方法ですね!
今回、データの特徴を表す統計量としてデータの代表的な値(代表値)を考えます。統計学基礎編では、代表値として「平均」を使います。

平均は日常でもよく使われますね。!全部の値を合計して、その数で割ればいいんですよね。
その通りです。
それではこのデータの平均を計算して頂けますか。
あるデータの観測値
2、1、6
はい!
まず合計を計算します。2 + 1 +6 = 9。
そして観測値の数3で割って、、、平均は3です!
その通りです。計算はもうかんぺきですね
やったあ!

それでは、別の視点で平均の意味を考えてみましょうか
別の視点、ですか?
偏差
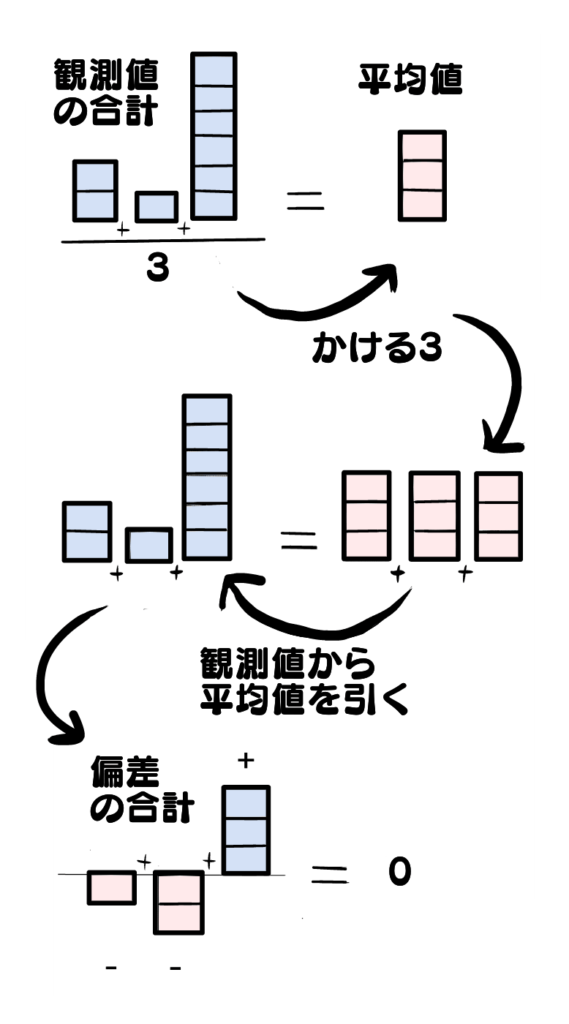
今、がるたろうくんは以下の計算をしてくれましたね

はい!このイメージです
データの観測値に関する情報を全部使って1つの代表的な値を求めていますね。
これを別の視点で見ていきましょう。
この関係は以下と同じことですね。数式上では、両辺に3をかけたことと同じです

確かにこうなりますね!
これは、「3個の個性的な値(左辺)を3個の平均的な値(右辺)に変換した」あるいは「もともとバラバラだった観測値の個性を無くした」とも解釈できます。

あっこれが最初に言っていたトンボかけのイメージにつながるわけですね。もともと凸凹な地面を真っ平らにする感じ。
個性をなくすと考えると観測値がかわいそうですね
それでは、平均値にすることで失った各観測値の個性を探しにいきましょう。右辺の数値を左辺にもっていくとどうなりますか?
それぞれの観測値から平均値を引けばよいですね
えーと、
(2 – 3), (1 – 3), (6 – 3) で、- 1 , – 2 , + 3 となりました!
元々小さな値はマイナスに、大きな値はプラスになります

右辺から左辺にもってきているので合計はゼロになりますね!何だか不思議な式になりました。どのように解釈したらよいでしょうか
観測値と平均の差を、観測値の「偏差」と言います。これは個々の観測値が、全体の中で平均より大きいのか小さいのかを示す指標です。

偏差はとても重要な用語なので覚えておきましょう!
重要!メモメモ…!
偏差の合計はゼロになります。この関係は、どんなデータでも必ず成り立ちます。なぜなら、平均値の計算式の定義そのものだからです。
平均値は、観測値の偏差の合計をゼロにするように決まる、これが平均の別の視点からのとらえかたです。
何だか不思議ですが、平均っていうのはそうなるように作られている数値ということですね。
おさらいしておきましょう。
観測値を分解
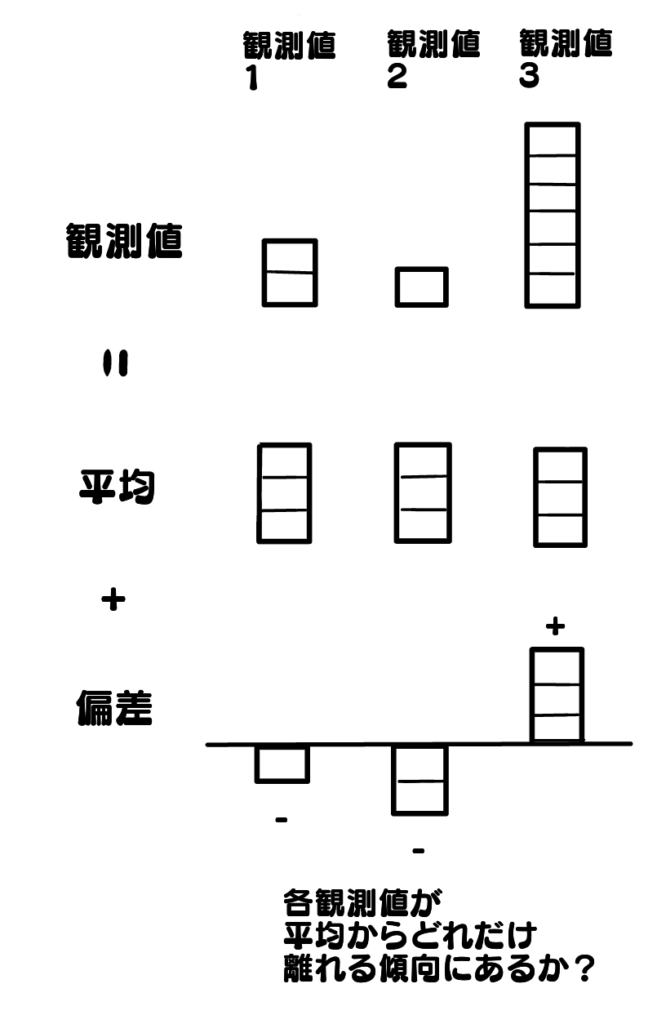
平均と偏差を学びました。今度は、これらを使って、観測値を別の視点で見てみましょう。
観測値も別の見方ができるんですか!
観測値は、平均と偏差の2要素からなっていると見れます。その解釈は、観測値はデータの分布の特徴となる2つの情報を含んでいるということです。
そういう見方ができるんですね!
平均は値の代表値の統計量で、、、偏差は、、、
観測値の偏差は、分布の重要な特徴である「値がどれくらいバラけるのか」を示す重要な情報源となります
平均が同じデータでも、偏差が大きい観測値を多く含むデータと、少ないデータでは、分布の特徴が大きく異なります。
もう一つの、観測値のばらつき具合を表す統計量につながるわけですね!
その通りです。具体的な計算は次回学んでいきましょう。
まとめ
本日はここまでにしておきましょう。平均と偏差、観測値の見方についてご紹介しました。
平均の違う見方が学べました!偏差という新しい考え方もでてきたので、しっかり復習しておきます!
がるたろうは
今日もたくさん学べたようです!
- データの分布の代表的な値として平均を使う。平均の別の見方を教わった。
- 観測値と平均の差を、観測値の「偏差」と言う。これは個々の観測値が、全体の中で平均より大きいのか小さいのかを示す指標。平均値は、観測値の偏差の合計をゼロにするように決まる
- 観測値は、平均と偏差の2要素からなっていると見れる。観測値の偏差は、分布の重要な特徴である「値がどれくらいバラけるのか」を示す重要な情報源。
今回扱った平均は、算術平均(相加平均)と言われるものです。他にも値の代表値の候補は色々あって、扱うデータの種類によって使い分けします。統計学の基礎編では算術平均のみを扱っていきます。
- 幾何平均(相乗平均):掛け算して意味がある値を分析する場合(経済の成長率、売上の増加率、気温の変化率など)
- 調和平均:比率として計算された値を分析する場合(株価と収益率の比率で投資する株式銘柄の構成を考える場合など)
- 中央値:左右対称でない分布、異常に大きかったり小さかったりする値も含むデータを分析する場合(所得、体重の分布など)


